Fisika klasikotik kuantikara: Potentziala eta kuantizazioa

Ion Abad, Mikel Arranz, Asier Goitia eta Beñat Txueka.

Mundu kuantikoa lege fisiko ezberdinek arautzen dute klasikoarekin alderatuz. Mundu kuantikoa, molekulen, atomoen, eta partikula azpiatomikoen mundua, deskribatzen duen teoria, Mekanika Kuantikoa da. Teoria honen ekuazioak ezagunak dira, baina gehienetan, ekuazio hauen soluzio zehatzak ezin dira lortu. Hori dela eta, ekuazioen soluzio hurbilduak bilatzen dira fisikan eta kimikan. Hala ere, ekuazioetatik ikasteko beste bide bat ere badago. Soluzio zehatza duten eredu idealak erabil daitezke. Eredu ideal hauek ez ditugu naturan aurkituko, baina naturan gertatzen diren hainbat fenomeno ulertzeko baliogarriak izaten zaizkigu. Bi eredu oso sinpleetan oinarriturik, kuantizazioaren natura azalduko dugu gaurkoan.

Bi eredu hauetan, partikula bakarra (kuantikoa zein klasikoa) izango dugu protagonista, potentzialezko kaxa batean itxita ala aske, beste deusekin elkarrekintza izan gabe. Azken kasu honetan fijatuko gara, abiapuntu gisa.

Partikula askeak: Infinitua eta uhinak.

Masa jakin bat duen partikula aske dagoenean, beste deusen eraginik ez du jasotzen. Mundu klasikoan bektore baten bidez irudikatu ohi dugu, honen ibilbidea jarraitzeko.

Partikularen abiadura jakinik, uneoro bere posizioa jakin dezakegu. Hau da, mundu klasikoan, partikularen abiadura eta posizioa zehaztuta daude. Horretaz gain, partikulak edozein abiadura izan dezakeenez, edozein energia izan dezake.

Mundu kuantikoan ordea, partikula uhina da ere, eta uhin-funtzio batek bere propietateak deskribatuko ditu. Kuantikaren ekuazioak askatuta, uhin-funtzio hau espazio osoan zehar hedatzen dela lortzen dugu, abiadura guztiz finkatu dezakegula lortuz. Beraz, partikula aurkitzeko probabilitatea berdina izango da espazioko puntu guztietan (uhin-funtzioaren karratuak ematen digu probabilitatea). Hortaz, partikularen abiadura ezagututa, ezin dugu deus jakin bere posizioari buruz (edozein lekutan egon daiteke!). Ondoko bideo laburrean hau ikus dezakezue, Heisenbergen ziurgabetasun printzipioa agertzen zaigularik.

Laburbilduz, partikula kuantiko askearen kasuan, honek edozein abiadura izan dezake (hortaz, edozein energia), baina abiadura jakinda ezin dugu deus esan bere posizioari buruz, eta partikula klasikoan ez-bezala, ezin dugu aurresan non egongo den edozein unetan. Fenomeno hau eredu ideal batean ikusi dugu, baina errealitatean ere gertatzen da.

Partikula kutxa batean

Azter dezagun orain bigarren eredu ideala, partikula kutxa batean. Demagun gaupasan ibili zarela gauean eta etxera iristen zarela. Argiak begietan min egiten dizu eta ezin duzu logelako argia piztu. Logela hankazgora daukazu eta pijama (gure partikula) bilatu behar duzu. Hau arazoa... Mundu klasiko batean pijama logelako edozein gainazalen gainean egon beharko litzateke. Hau da, gela osoan bueltaka ibiliko zinateke ero moduan hau topatu edo nazkatu eta kaleko arropekin oheratu arte. Zorionez kuantikak lan hori murriztu dezake zuretzat.

Itxita dagoen kaxa batek zure logelaren eredutzat hartuko dugu, non gure partikula kaxa honetatik ezin den atera inolaz ere, zure pijamaren moduan (amak garbigailuan sartu ez badu noski). Kasu honetan, kuantikaren ekuazioak askatzean, ondorengo soluzio zehatzak lortzen ditugu. Partikularen energia, orain, mailakaturik dago, eskailera batzuk izango balira bezala (eta ezin da zero izan!). Maila horiek irudikatzeko pentsa ezazu eskailerak igo behar dituzula, eta eskailera horiek, finkatutako mailetan igo edo jaisten dituzu, banaka, binaka eta ahal duenak hirunaka edo gehiagotan baina inoiz ez erdizka edo osoa ez den kopuruetan. Partikulekin berdina gertatzen da, energia mailak finkatuta (mundu kuantikoan kuantizatuta) daudelako, eta partikularen energiak ezin du beste edozein balio hartu. Hortaz, partikula askearekin alderatuta, energia kuantizatuta dagoela lortzen dugu. Bestalde, pijamarekin alderatuta (geldirik dago), gure partikula ezin da geldirik egon! (energia ez delako zero inoiz).

Baina sorpresak ez zaizkigu agortu oraindik! Honela, kutxara itzuliz, energia maila bakoitzari dagokion uhin-funtzioa azter dezakegu. Beheko irudian, dimentsio bakarrean uhin-funtzio hauen forma ikus dezakezue. 1 zenbakia duena lehenengo energia mailari dagokio, 2 zenbakia duena bigarrenari, eta abar.

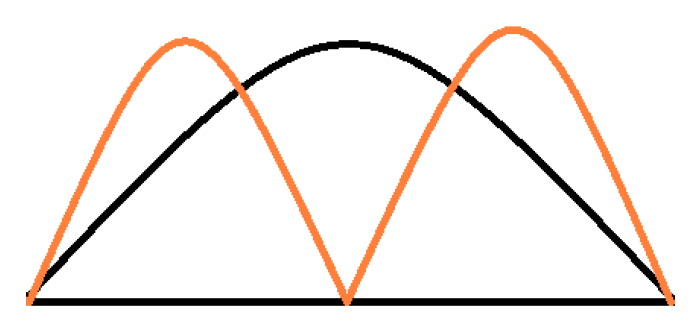
Lerro edo funtzio hauek gure partikula kutxa barruan aurkitzeko “pistak” ematen dizkigute. Izan ere funtzioen karratua eginez gero, partikula kutxa barruan aurkitzeko probabilitatea lortuko dugu. Ondorengo grafikoan ikus daitezke 1 eta 2 energia mailei dagozkien berbidurak. 

• 1 energia mailari dagokion lerroari so egiten badiogu arku itxura duela ikus daiteke. Arku honen baliorik altuena edo maximoa erdialdean dago, eta hortik ondoriozta dezakegu partikula aurkitzeko probabilitate maximoa kutxaren erdian dagoela.

• 2 energia mailari erreparatuz aurrekoarekin desberdintasun batzuk nabari dira. Maila honetan tontor bat izan ordez bi tontor ditugu eta bi hauek elkartzen diren puntuan nodo bat aurkitzen da (funtzioak 0 balioa hartzen du). Beraz, partikula aurkitzeko probabilitate maximoa bi puntutan izango dugu eta ez baten soilik. Horretaz gain badugu kutxaren puntu jakin bat non partikula aurkitzeko probabilitatea nulua izango den. 

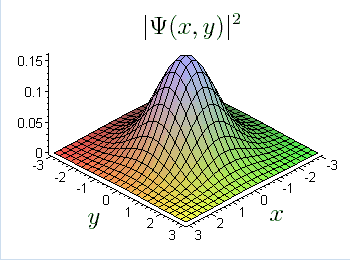
Hortaz, gure pijama kuantikoa izanen balitz, gaupasa egin eta gero aurkitzeko probabilitate handiagoa izanen genuke, gelako puntu konkretuetan bilatuz. Goiko dimentsio bakarreko adibideak, gure bi dimentsiozko logelan baliokideak dituzte. Adibide gisa, ondoko irudia duzue. Pijama aurkitzeko probabilitatea irudikatzen dugu, oinarrizko egoeran (energia minimoko egoeran). Hau da, pijama kuantikoa balitz, gela erdian aurkitzeko probabilitatea maximoa litzateke.

Laburbilduz, mundu kuantikoan propietateen kuantizazioa ez da kasu guztietan ematen, partikula konfinatzean ikusten dugun zerbait baizik.

________________________________________________________

Egileak: Ion Abad, Mikel Arranz, Asier Goitia eta Beñat Txueka UPV/EHUko Kimika Fakultateko ikasleak dira. Kimika Fisikoa II irakasgaian egindako lana.
________________________________________________________

Sarrera honek #KulturaZientifikoa 1. Jaialdian parte hartzen du.

Descargo de responsabilidad: He utilizado las imágenes sin ánimo de lucro, con un objetivo de investigación y estudio, en el marco del principio de uso razonable - sin embargo, estoy dispuesto a retirarlas en caso de cualquier infracción de las leyes de copyright.Disclaimer: I have used the images in a non for profit, scholarly interest, under the fair use principle - however, I am willing to remove them if there is any infringement of copyright laws.